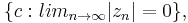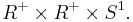Parameter space
In science, a parameter space is the set of values of parameters encountered in a particular mathematical model. Often the parameters are inputs of a function, in which case the technical term for the parameter space is domain of a function.
Parameter spaces are particularly useful for describing families of probability distributions that depend on parameters. More generally in science, the term parameter space is used to describe experimental variables. For example, the concept has been used in the science of soccer in the article "Parameter space for successful soccer kicks." In the study, "Success rates are determined through the use of four-dimensional parameter space volumes."[1]
In the context of statistics, parameter spaces form the background for parameter estimation. As Ross (1990) describes in his book:
- Parameter space is a subset of p-dimensional space consisting of the set of values of Θ which are allowable in a particular model. The values may sometimes be constrainted, say to the positive quadrant or the unit square, or in case of symmetry, to the triangular region where, say
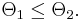
The idea of intentionally truncating the parameter space has also been advanced elsewhere.[2]
Contents |
Examples
- In complex dynamics the parameter space is the complex plane
- C = { z = x + y i : x, y ∈ R }
where i2 = −1. The famous Mandelbrot set
where z0 = 0, and for n > 0, 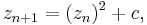 is a subset of this parameter space. The function
is a subset of this parameter space. The function 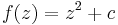 is a complex quadratic polynomial.
is a complex quadratic polynomial.
- In a sine wave model
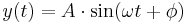
the parameters are amplitude A > 0, angular frequency ω > 0, and phase φ ∈ S1. Thus the parameter space is
History
Parameter space contributed to the liberation of geometry from the confines of three-dimensional space. For instance, the parameter space of spheres in three dimensions, has four dimensions -- three for the sphere center and another for the radius. According to Dirk Struik, it was the book Neue Geometrie des Raumes (1849) by Julius Plücker that showed
- ...geometry need not solely be based on points as basic elements. Lines, planes, circles, spheres can all be used as the elements (Raumelemente) on which a geometry can be based. This fertile conception threw new light on both synthetic and algebraic geometry and created new forms of duality. The number of dimensions of a particular form of geometry could now be any positive number, depending on the number of parameters necessary to define the "element".[3]
The requirement for higher dimensions is illustrated by Plücker's line geometry. Struik writes
- [Plücker's] geometry of lines in three-space could be considered as a four-dimensional geometry, or, as Klein has stressed, as the geometry of a four-dimensional quadric in a five-dimensional space.[4]
See also
Notes and references
- ^ Cook & Goff (2006)
- ^ Van Eeden, C. (2006)Restricted parameter space estimation problems: admissibility and minimaxity properties, Springer ISBN 0387337474 (p. 2) "Gains in the minimax value can be very substantial when the parameter space is bounded."
- ^ Struik (1967) 165
- ^ Struik (1967) 168
- Brandon G. Cook & John Eric Goff (2006) Parameter Space for Successful Soccer Kicks European Journal of Physics 27:865.
- Constance van Eeden (2006) Restricted Parameter Space Estimation Problems: Admissibility and Minimaxity Properties, Lecture Notes in Statistics #188, Springer Science+Business Media.
- Gavin J.S. Ross (1990) Nonlinear Estimation, page 94, Springer-Verlag.
- Dirk Struik (1967) A Concise History of Mathematics, 3rd edition, page 165, Dover Books.